Everything You Need to Know About SAT Function Problems

Function questions are among the hardest types of questions you'll encounter on the SAT Math section. They often appear complex, require a solid understanding of advanced math concepts, and may involve multiple steps to solve. Additionally, many students lack prior experience or sufficient practice with functions, making these questions seem even more daunting.

Thankfully, there’s a way to make SAT function questions much less overwhelming. By familiarizing yourself with their basic principles and understanding the common types of function problems found on the SAT, you can approach these questions with greater confidence. This is invaluable because you're likely to come across at least ten function-related questions during the SAT Math section.

Keep reading to discover what functions are, the four main types of SAT function questions, step-by-step strategies for solving them, and helpful tips to simplify even the toughest function problems.

What Are Functions?

Before diving into specific SAT function questions, let’s revisit the fundamental concept of functions. Having a strong foundation in this area will make tackling SAT function problems much easier.

Simply put, a function is a rule that takes an input, applies a certain operation or process, and produces a corresponding output. Think of a function as a vending machine: you press a button (input) and receive a specific snack (output). Each time you press the same button, you’ll always get the same snack. However, pressing a different button will result in a different snack.

Each input (x-value) corresponds to only one output (y-value), although a single output may be associated with multiple inputs. In other words, different inputs can produce the same output. Returning to the vending machine example, pressing button B12 might always give you "Cool Ranch Doritos." No matter how many times you press B12, the output remains the same. But since Cool Ranch Doritos are so popular, the vending machine might assign them to multiple buttons (e.g., B12 and C4). This means that even though the output (Cool Ranch Doritos) is the same, there are multiple inputs (buttons B12 and C4) that can lead to it.

This also explains certain properties of a function graph. A function can have multiple x-intercepts, but only one y-intercept. This is because when the input is x=0, there can only be a single output or y-value.

Functions are often represented using function notation: f(x)=_____. In this format, f denotes the name of the function, x represents the input, and the expression after the equals sign specifies what operation is performed on that input.

For example, if the function is written as f(x)=x+5, it means that for any number you substitute into x, the function will add 3 to it. So：

f(3)=3+5=8

f(11)=11+5=16

Note: A function doesn’t always have to be named f. The example above uses f, but it’s also common to see functions written as h(x), g(x), r(x), or any other name.

For instance, take the function:
h(x)=8(x−3)+5

- g: The name of the function

- x: The input

- 8(x−3)+5: The rule or expression that produces the output when you substitute a value for x.

An ordered pair in functions refers to pairing a specific input with its corresponding output. Let’s find the ordered pair for the example above when the input is x=5:

h(5)=8(5−3)+5

=8(2)+4

=16+4

=20

Thus, the ordered pair for this function is (5,20).

Graphing Functions

Functions can always be represented visually as graphs, and the shape of the graph changes depending on the type of function. On a standard coordinate plane, where the axes are labeled x and y:

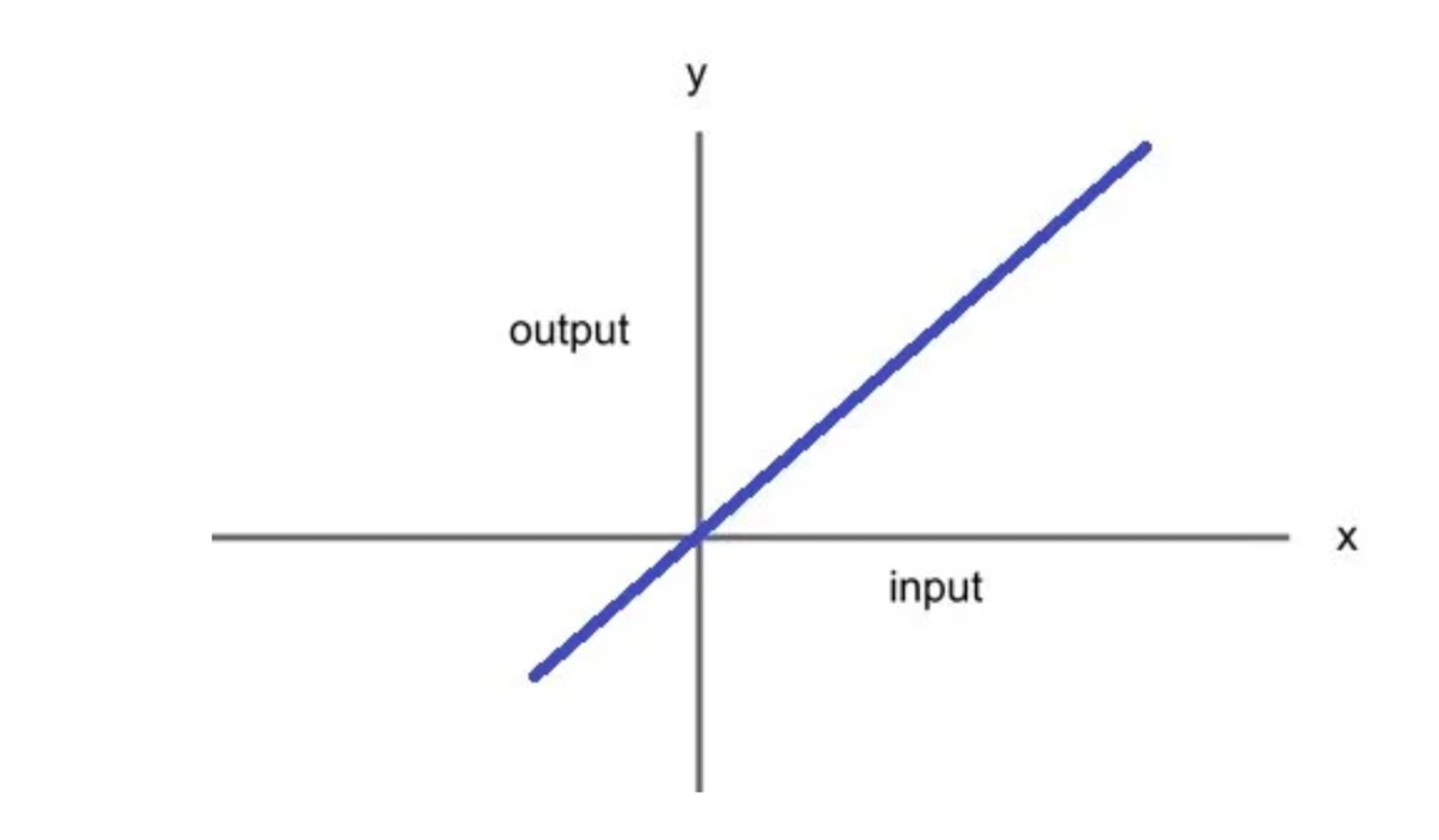
It’s important to remember that a function graph can have multiple x-intercepts because different inputs may lead to an output of y=0. However, a function will always have only one y-intercept since there is only one output when x=0.

Linear Functions

A linear function produces a graph in the shape of a straight line. The example shown in the graph above is a representation of a linear function.

For linear functions, the x-variable is never raised to a power higher than 1 (e.g., there’s no x^2, x^3, or similar terms). This is what distinguishes linear functions from other types, such as quadratic or cubic functions.

The equations of linear functions typically look like the following examples:

y=2x+5

g(x)=−3x+7

f(x)=21​x−4

Quadratic Functions

A quadratic function creates a graph in the shape of a parabola. In these functions, the output variable always involves the square of the input x^2.

It’s important to remember that when squaring a number, both a positive and a negative input result in the same value. For example:

(2)^2=4 and (−2)^2=4

This property explains why quadratic functions have a parabolic curve: there are two inputs (one positive and one negative) for every output, except at the vertex of the parabola.

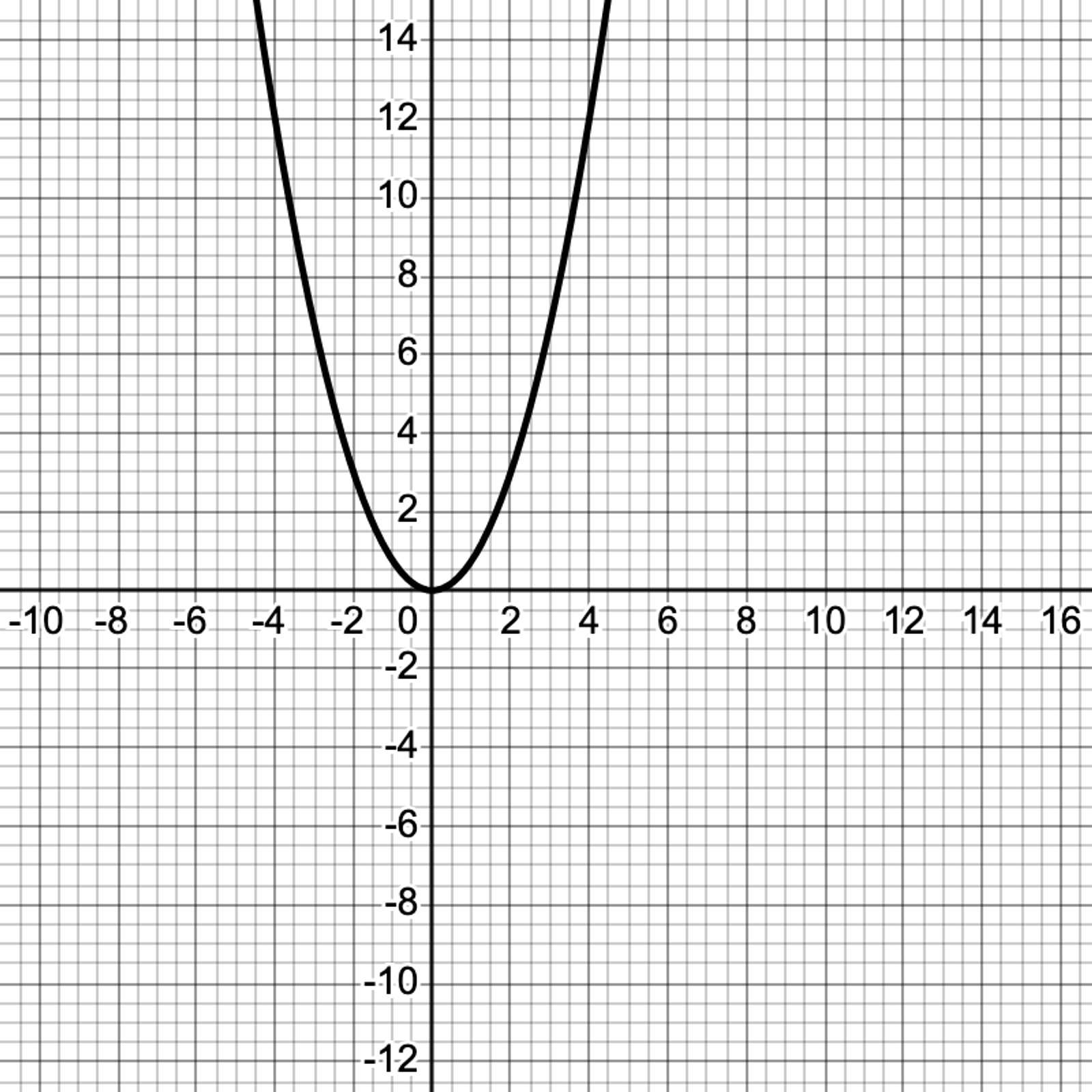
A quadratic function is usually written as:

f(x)=ax^2+bx+c

The value of a determines the shape of the parabola and the direction it opens.

A positive a gives a parabola that opens upward, like the graph above.

A negative a gives a parabola that opens downward, like this graph:

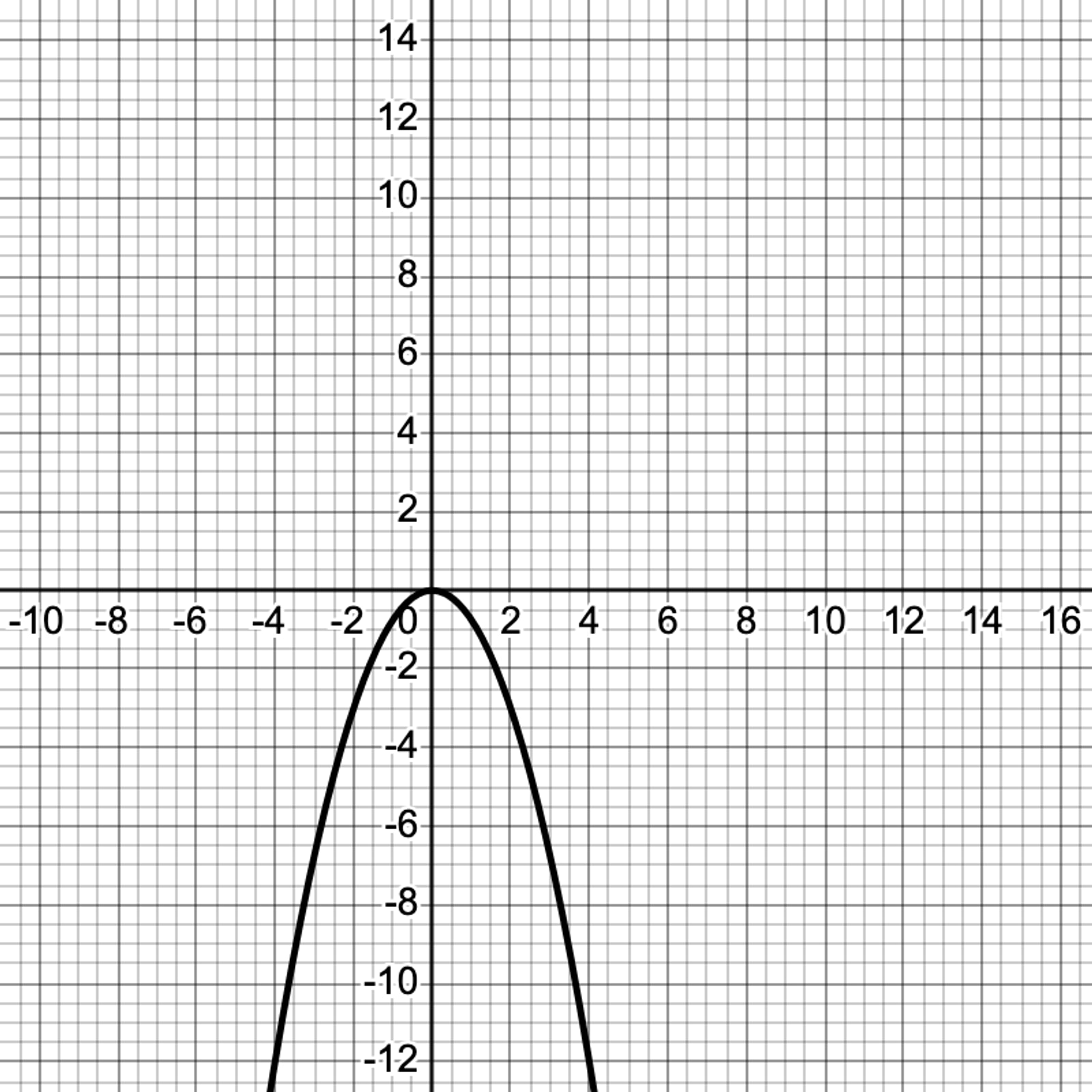
The larger the a-value is, the "skinnier" the parabola becomes.

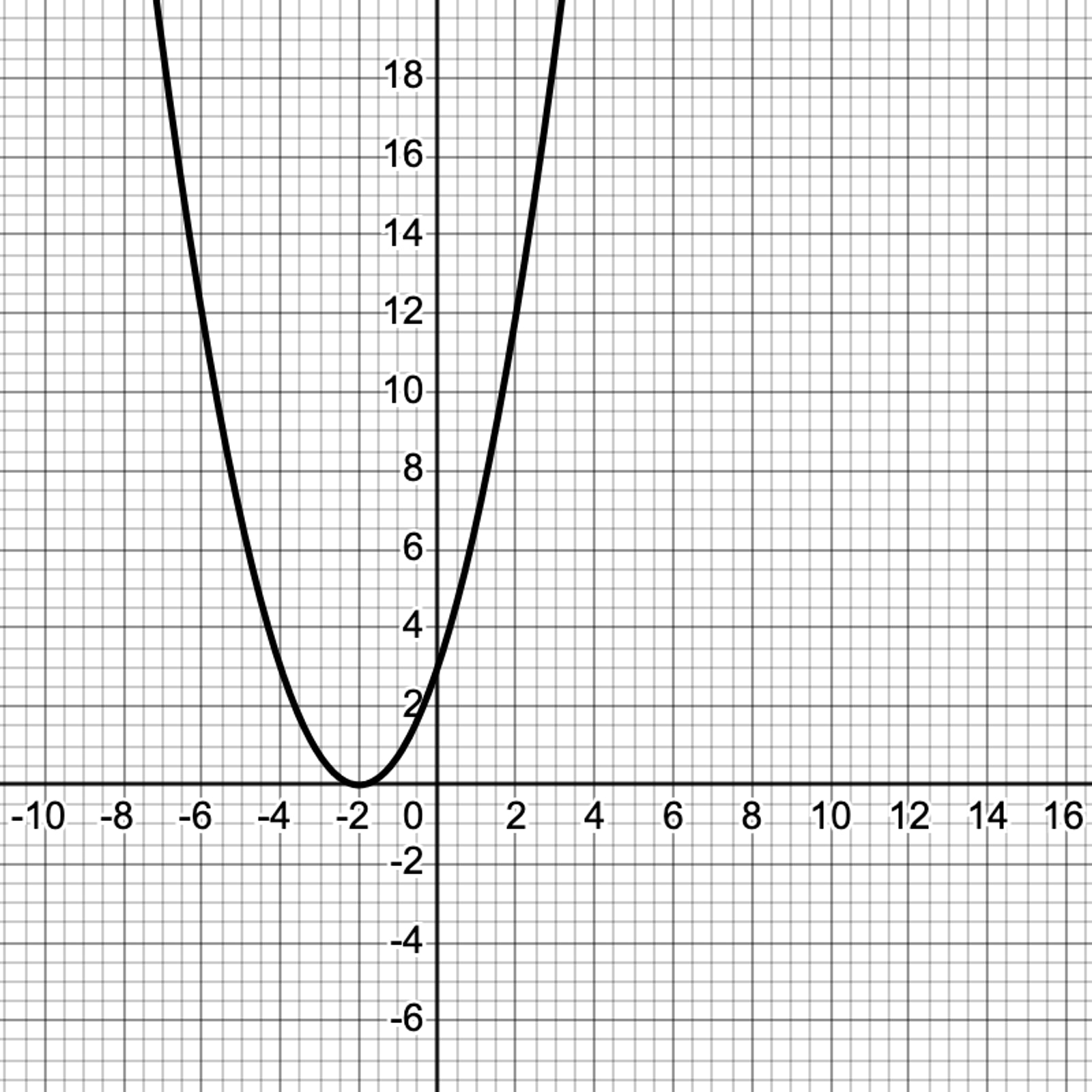
The b-value determines the position of the vertex of the parabola, either to the left or right of the origin.

A positive b places the vertex of the parabola to the left of the origin:

A negative b places the vertex of the parabola to the right of the origin:

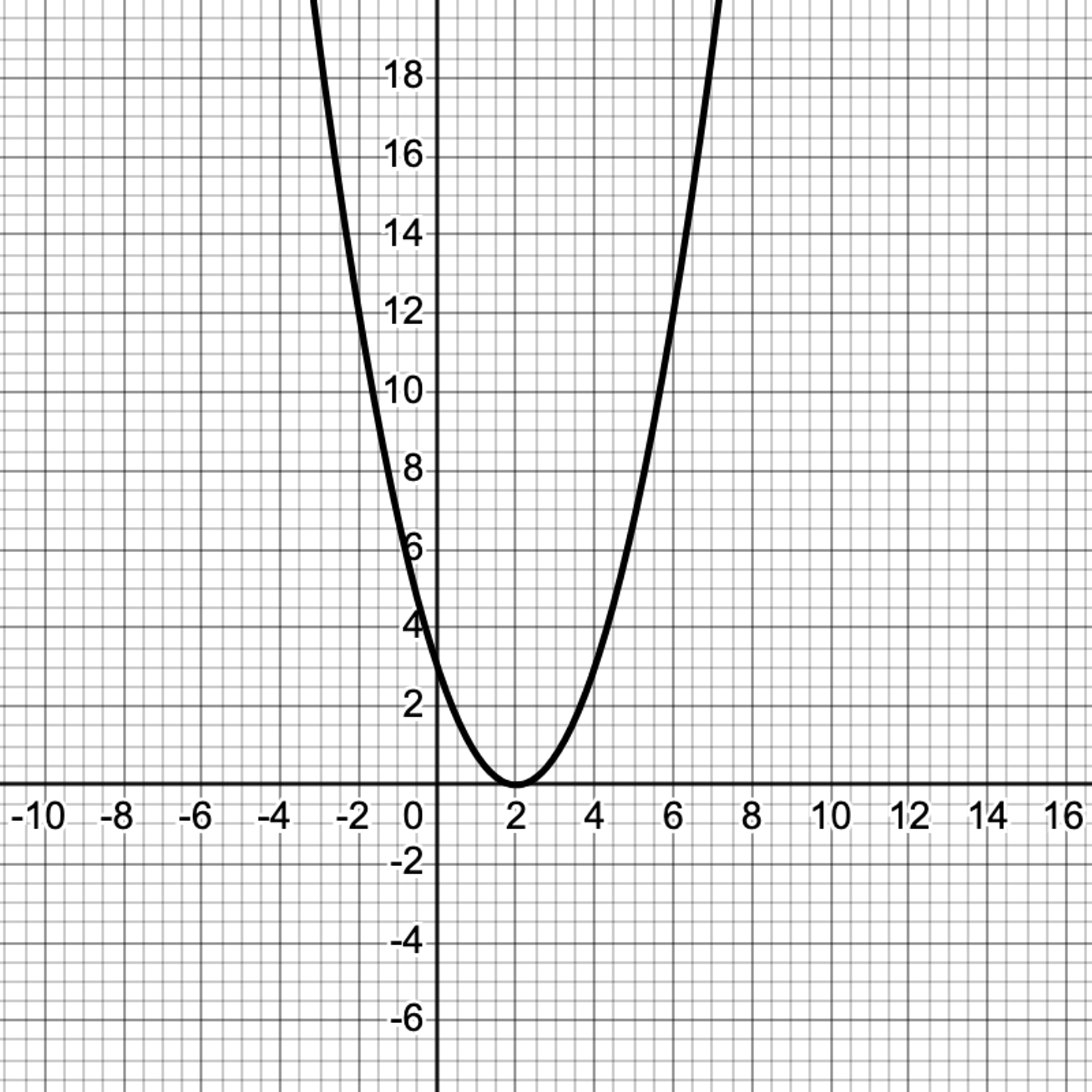
The c-value represents the y-intercept of the parabola. This is where the graph crosses the y-axis. In the graph below, the red dot indicates the y-intercept:

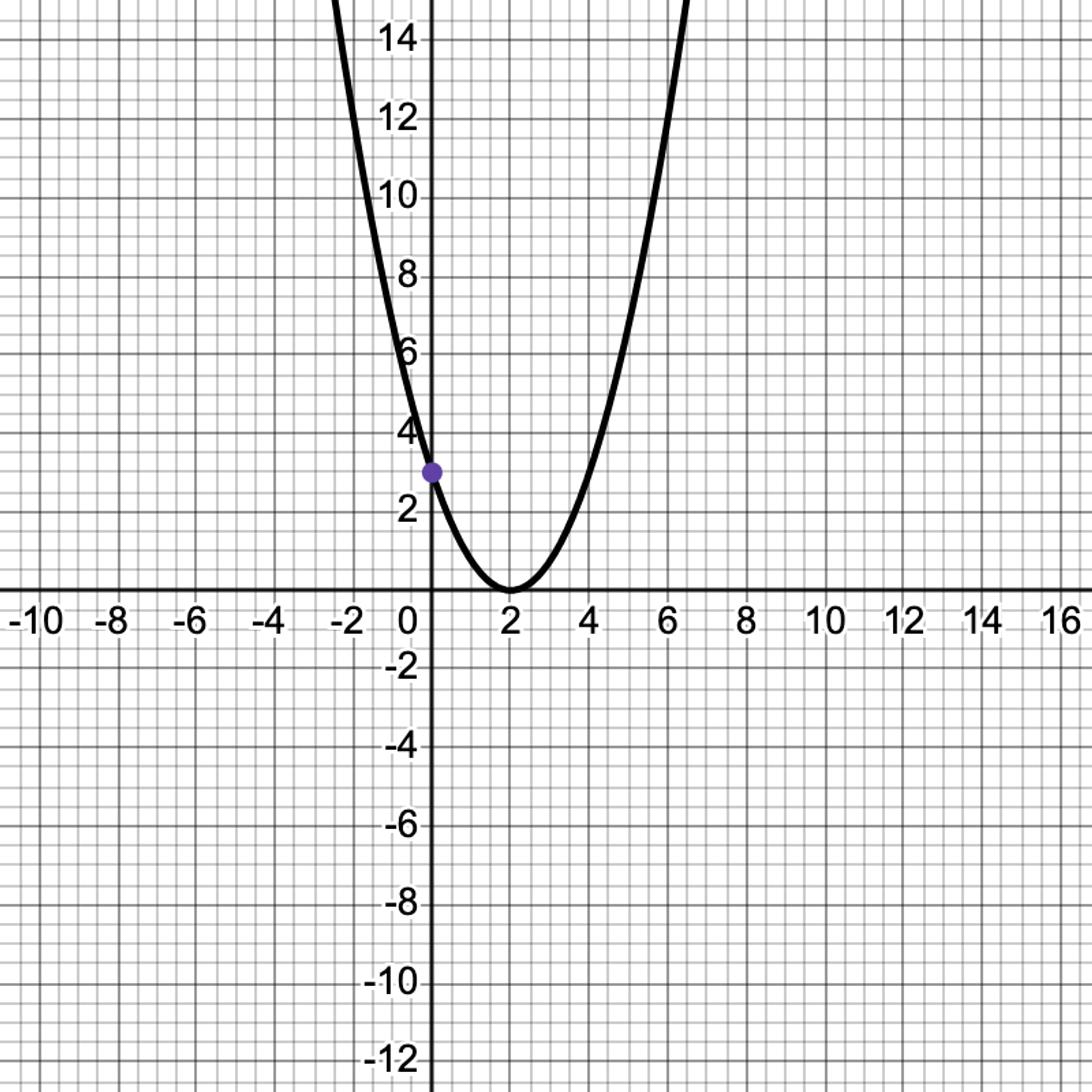
Note: When b=0, the y-intercept also becomes the location of the vertex of the parabola, as shown here:

Function Questions on the SAT: 4 Examples

Let’s take a look at what function-related questions typically look like on the SAT. Generally, there are four types of SAT function questions. Below, we explain each type and provide an example, with all examples sourced from official SAT practice exams.

1.Function Equations

These are the most common function problems you’ll encounter on the SAT, with likely at least six appearing on your exam. A function equation problem presents a function in equation form, then asks you to use one or more inputs to determine either the output or parts of the output.

Example:

Explanation:

This is a grid-in problem, meaning you’re not given answer choices; instead, you must calculate and enter your own answer.

To solve for the specific output, we need to plug the given input for x into the equation. We’re informed that the point (24,0) lies on the graph of y=g(x), which means g(24)=0. This tells us that when x=24, the function g(x) equals 0. So, we substitute x=24 into the function:

g(24)=(24+14)(t−24)

Since g(24)=0, we set the entire equation equal to 0:

(24+14)(t−24)=0

Simplify the expression:

38(t−24)=0

For this equation to hold true, either 38=0 (which is impossible) or t−24=0. Thus:

t=24

Now substituting t=24 into the function gives:

g(x)=(x+14)(24−x)

To find the value of g(0), substitute x=0 into the equation:

g(0)=(0+14)(24−0)

Simplify:

g(0)=(14)(24)
g(0)=336

Therefore, the final answer is: 336​

2. Function Tables

The second way functions can appear on the SAT is in the form of a table. In these problems, you may either:

Be given a table of input and output values and asked to determine the equation of the function, or

Be provided with a function equation and asked to identify which table of values corresponds correctly to the function (as in the example below).

Explanation:

We are given the function h(x)=x^2−3 and four tables to choose from. Each table has x-values of 1, 2, and 3, and our task is to determine which table correctly matches the outputs of the function.

Step 1: Substitute x=1 into the function

h(1)=1^2−3=1−3=−2

So, when x=1, h(x)=−2.

- Looking at the tables, Choices A and C are incorrect because their output for x=1 isn't −2.

- We’re now left with Choices B and D.

Step 2: Test x=3 to narrow it down further

Substitute x=3 into the function:

h(3)=3^2−3=9−3=6

So, when x=3, h(x)=6.

Looking at the remaining options, only Choice B has the expected output of h(x)=6 for x=3.

Answer:

The correct table is Choice B!

3: Function Graphs

These questions will typically ask you to identify specific elements of a graphed function or determine the equation of the function from the graph. Function graph questions might seem intimidating, but they're often the easiest type of SAT function question. Just remember that x is your input, and the equation gives your output, y.

Function graph questions are also the least common type of function problem on the SAT. At most, you’ll encounter two, but it’s more likely that you’ll see only one or even none on your test.

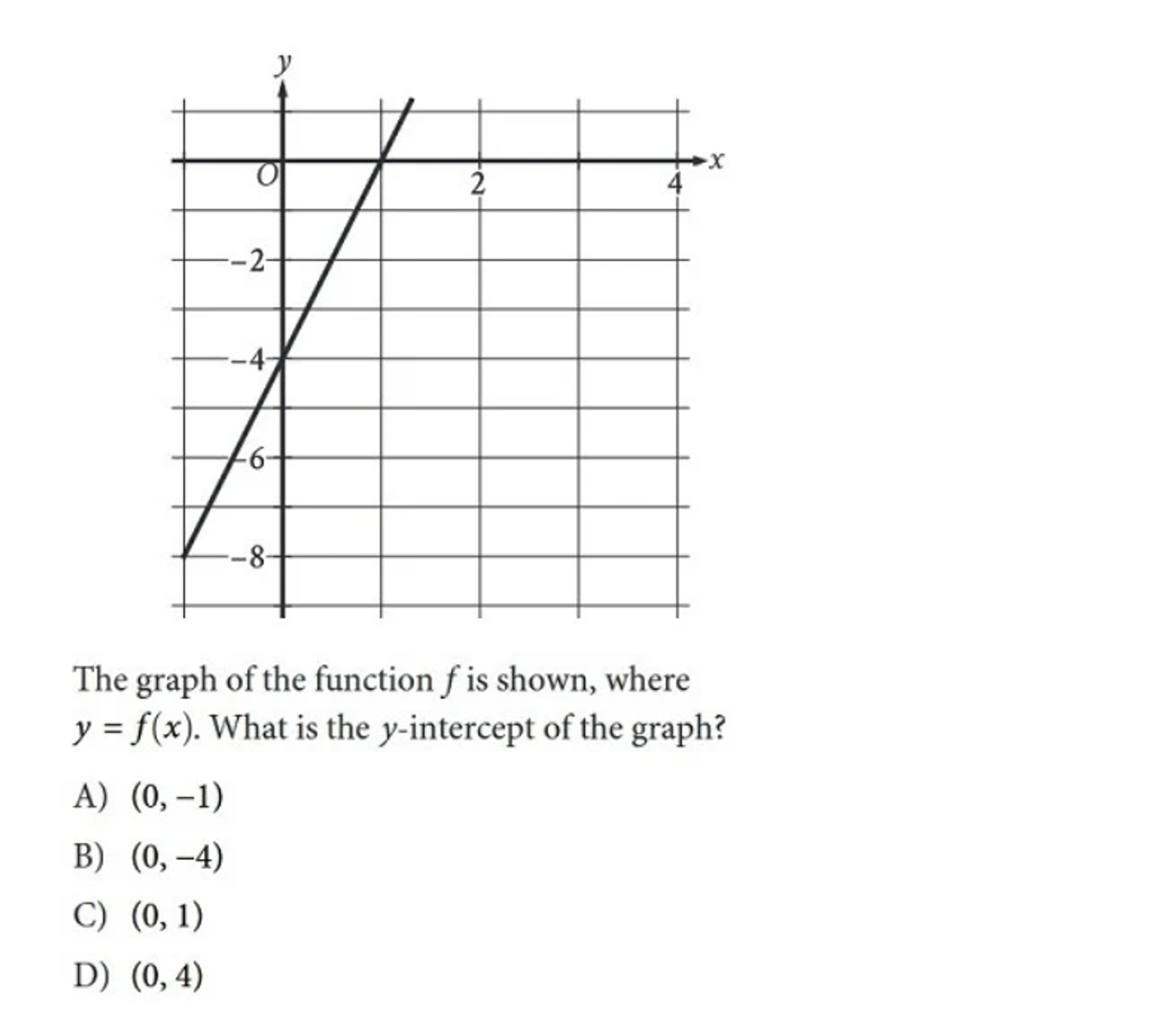
Explanation:

By definition, the y-intercept of a graph is the point where the graph intersects the y-axis. The graph of the given function intersects the y-axis at (0,−4). Therefore, Choice B is the correct answer. Easy!

4.Function Word Problems

This is one of the newer types of SAT function questions, and you can expect to see 2 to 3 of these on the test. For these problems, you won’t solve equations or perform calculations. Instead, you’ll be given a function and asked to choose the "best interpretation" of a specific part of it. These questions test your understanding of functions and what their different components represent, rather than your ability to perform complex math.

Example:

Explanation:

We know that the function f(t)=14t+9 gives the estimated length of a plant, where t represents the number of months ago the plant was purchased.

From what we know about functions, when a function is in the form f(t)=mt+b, the b-value represents f(0), which is the value of f(t) when t=0. In this case, b is 9. Therefore, the 9 represents the value of f(t) when t=0. Since f(t) represents the length of the plant and t is the number of months ago the plant was purchased, t=0 means the plant was just purchased. Thus, the plant was 9 inches long when it was purchased. The function also shows that the plant grows longer by 14 inches each month.

Therefore, the best interpretation of 9 is that the vine was 9 inches long when Tavon purchased it, or Choice D.

Why the Other Choices Are Incorrect:

-Choice A: Incorrect because there’s nothing in the function that refers to how long Tavon will keep the vine.

-Choice B: Incorrect because the vine is growing 14 inches per month, not 9 inches.

-Choice C: Incorrect because there’s no indication in the function of a maximum length the vine will grow.

4 Must-Know Strategies for Tackling SAT Function Questions

Now that you’ve seen the different types of function problems that might appear on the SAT, let’s dive into some specific strategies to effectively and efficiently solve them.

1.Leverage Plugging In Answers (PIA) and Plugging In Numbers (PIN)

For many function-based problems, you can simplify your work by testing answer choices directly using Plugging In Answers (PIA). This strategy lets you work backward to verify whether an answer choice satisfies the given function.

For variable-heavy questions, use Plugging In Numbers (PIN). By substituting simple values for the variables in the function, you can test different points or scenarios with ease. This is especially handy when solving:

- Problems involving graphs of functions.

- Questions where the answers are expressed in terms of variables.

Pro Tip: Whenever answer choices include variables, PIN is a highly effective go-to strategy.

2. Using the FOIL Method for Solving Function Equations

The FOIL method (First, Outer, Inner, Last) is a helpful tool when multiplying binomials, especially in SAT problems involving function equations. Here’s a quick breakdown of how it works:

Example: Multiply (x+2)(3x−5) Using FOIL

First Terms: Multiply the first terms in each binomial: x⋅3x=3x^2

Outer Terms: Multiply the outer terms: x⋅(−5)=−5x

Inner Terms: Multiply the inner terms: 2⋅3x=6x

Last Terms: Multiply the last terms: 2⋅(−5)=−10

Using FOIL, we get the product as: 3x^2+x−10​

Common Mistakes to Watch Out For:

One frequent error occurs when squaring a binomial. For example, with the expression (x+4)^2, some students incorrectly write: (x+4)^2=x^2+16. This is wrong! To find the correct solution, you must treat (x+4)^2 as (x+4)(x+4) and use FOIL, the correct answer is: x^2+8x+16.

3. Start by Finding the Y-Intercept

When working with function graphs or tables, the best place to start is usually by identifying the y-intercept. This is often the simplest feature of the graph or equation to find and can help you narrow down the answer choices right away.

The y-intercept is the point where the graph crosses the y-axis (where x=0). Look for this information in the table, graph, or equation provided. Once you determine the y-intercept, you can easily eliminate any answer choices that don’t match.

Because it’s one of the easiest features to identify, always consider finding the y-intercept as your starting point when analyzing function questions.

4. Use Ordered Pairs to Test Your Equation

Another useful strategy is to find and verify multiple ordered pairs that satisfy your function. An ordered pair must work for both the equation and any given graph or table. Testing pairs ensures that the function applies universally, not just to one or two points.

For example, as seen in the function table question discussed earlier, one point might work for the equation while another does not. In such cases, you can quickly eliminate any incorrect equations or graphs.

Key Tip:

You must ensure that every ordered pair matches the equation, not just some. Functions are unique and consistent, so one mismatch indicates the function or graph is incorrect.

Summary: Tackling Functions on the SAT

While many students may feel unfamiliar with functions, don’t let these questions intimidate you! At their core, functions are about understanding inputs, outputs, and plugging in values—a concept that’s straightforward once you get the hang of it.

By focusing on the basic principles and applying strategies like identifying the y-intercept, using FOIL for multiplication, and testing ordered pairs, you can confidently solve SAT function questions.

If you’ve worked through the examples and quiz in this article, you’re in a great spot to master function questions on the SAT Math section. Practice, stay consistent, and you’ll excel!